Les complexes cellulaires permettent de créer une grande diversité de voisinage. L'un des avantages est notamment d'appliquer une transformation prévue pour une collection homogène (comme peuvent l'être les collections GBFs, où chaque élément à un nombre constant de voisins), sur une collection dont le voisinage peut varier.

A titre d'exemples, nous allons nous intéresser à l'application de transformations implantant les automates cellulaires sur des maillages géométriques tridimensionnels.

Diffusion limitée par agrégation

Il s'agit d'un automate cellulaire classique modélisant la diffusion de particules dans une milieu. Certaines des particules sont fixes tandis que d'autres se déplacent. Les deux règles régissant le comportement des particules sont extrêmement simples :

1. Agrégation : si une cellule mobile rencontre (= est voisine de) une particule fixe, elle s'agrège à cette particule et se fixe ;
2. Diffusion : si une particule mobile est voisine d'un emplacement vide, elle se déplace vers cet emplacement laissant celui qu'elle quitte vide.

Le code de cette transformation est le suivant :

On remarque que cette transformation ne dépend pas de la collection sur laquelle elle est appliquée.

Si DLA est appliquée sur un pavage hexagonal, la résultat est le suivant :

Cliquez sur l'image pour l'agrandir.
DLA sur une structure régulière : un pavage héxagonal.

Nous allons appliquer DLA sur une sphère où on considère les facettes comme les positions des particules. On considère également que deux facettes sont voisines si elles ont un arc en commun. On notera que ce voisinage est un voisinage de Von Neumann dans une pavage carré. En revanche, si on considère que deux facettes sont voisines si elles partagent un sommet, on obtient un voisinage de Moore pour la même organisation. Sur la sphère, le voisinage n'est pas constant. En effet, sur le maillage que nous utilisons, les pôles correspondent à des triangles, alors que les autres facettes sont des carrés. Aussi, pour certaines positions, le nombre de voisins est égal à 3 (aux pôles), ou à 4 pour d'autres. Les figures suivantes présentent l'état de la sphère à t=0, après quelques itérations et lorsque le point fixe est atteint :

On peut appliquer cette transformation sur d'autres objets : une bouteille de Klein dont la particularité est qu'elle n'est pas orientable, et un pion d'échec, topologiquement équivalent à un disque.

Des fourmis en quête de nourriture...

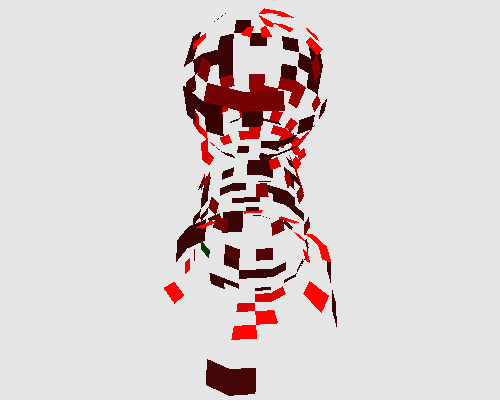
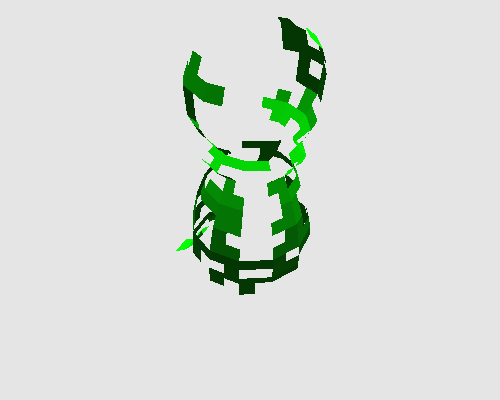
Dans ce second exemple, on reprend le modèle de simulation de comportement des fourmis cherchant de la nourriture décrit ici. Comme pour le DLA, on applique la transformation telle quelle sur une sphère. L'animation est téléchargeable ici (4.3 Mo). Les cellules noires sont des fourmis cherchant la nourriture, les jaunes des fourmis ayant trouvé de la nourriture et retournant vers le nid. Le nid est bleu et la nourriture en vert. Les traces rouges transparentes correspondent à des traînées de phéromone laissée par les fourmis rentrant au nid pour pouvoir retrouver la nourriture. Le degré de transparence reflète l'évaporation de cette substance.

this site is under construction.
Pages started: May 2002. Last revision: 24 jully 2003.

Pictures, graphics and animations are licensed under a Creative Commons License.